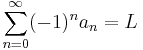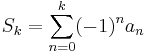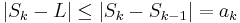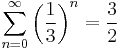Alternating series test

The alternating series test is a method used to prove that infinite series of terms converge. It was discovered by Gottfried Leibniz and is sometimes known as Leibniz's test or the Leibniz criterion.

A series of the form

$\sum_{n=0}^\infty (-1)^n a_n\!$

where all the a_n are non-negative, is called an alternating series. If the sequence a_n approaches 0 as n approaches infinity, and the sequence a_n is monotone decreasing (i.e. each a_n is smaller than a_n−1), then the series converges. If L is the sum of the series,

$\sum_{n=0}^\infty (-1)^n a_n = L\!$

then the partial sum

$S_k = \sum_{n=0}^k (-1)^n a_n\!$

approximates L with error

$\left | S_k - L \right \vert \le \left | S_k - S_{k-1} \right \vert = a_k\!$

It is perfectly possible for a series to have its partial sums S_k fulfill this last condition without the series being alternating. For a straightforward example, consider:

$\sum_{n=0}^\infty \left(\frac{1}{3}\right)^n = \frac{3}{2}\!$

1 Proof
- 1.1 Proof of convergence
- 1.2 Proof of partial sum error
2 See also
3 Literature
4 References
5 External links

Proof

^[1]

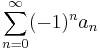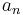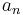We are given a series of the form $\sum_{n=0}^\infty (-1)^n a_n\!$ . The limit of the sequence $a_n$ equals 0 as $n$ approaches infinity, and each $a_n$ is smaller than 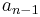$a_{n-1}$ (i.e. the sequence 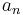$a_n$ is monotone decreasing).

Proof of convergence

The (2n+1)-th partial sum of the given series is 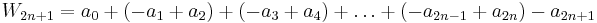$W_{2n%2B1} = a_0 %2B \left( { - a_1 %2B a_2 } \right) %2B \left( { - a_3 %2B a_4 } \right) %2B \ldots %2B \left( { - a_{2n - 1} %2B a_{2n} } \right) - a_{2n%2B1}$ . As every sum in brackets is non-positive, and as 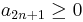$a_{2n%2B1} \geq 0$ , then the (2n+1)-th partial sum is not greater than $a_0$ .

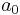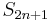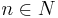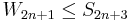That very (2n+1)-th partial sum can be written as $W_{2n%2B1} = \left( {a_0 - a_1 } \right) %2B \left( {a_2 - a_3 } \right) %2B \ldots %2B \left( {a_{2n} - a_{2n%2B1} } \right)$ . Every sum in brackets is non-negative. Therefore, the series $S_{2n%2B1}$ is monotonically increasing: for any $n \in N$ the following holds: $W_{2n%2B1} \le S_{2n %2B 3}$ .

From the two paragraphs it follows by the monotone convergence theorem that there exists such a number s that 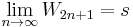$\lim_{n \to \infty } W_{2n%2B1} = s$ .

As 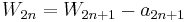$W_{2n} = W_{2n%2B1} - a_{2n %2B 1}$ and as 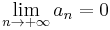$\lim_{n \to %2B \infty } a_n = 0$ , then 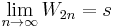$\lim_{n \to \infty } W_{2n} = s$ . The sum of the given series is 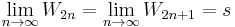$\lim_{n \to \infty}W_{2n} = \lim_{n \to \infty}W_{2n %2B 1} = s$ , where $s$ is a finite number. Thus, convergence is proved.

Another way to prove this is showing that the sequence of partial sums are a cauchy sequence.

Proof of partial sum error

In the proof of convergence we saw that 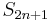$S_{2n%2B1}$ is monotonically increasing. Since 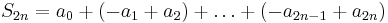$S_{2n} = a_0 %2B\left(-a_1 %2B a_2\right) %2B \ldots %2B \left(-a_{2n-1} %2B a_{2n}\right)$ , and every term in brackets is non-positive, we see that 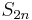$S_{2n}$ is monotonically decreasing. By the previous paragraph, 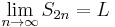$\lim_{n \to \infty}S_{2n} = L$ , hence 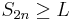$S_{2n} \geq L$ . 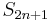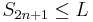Similarly, since $S_{2n%2B1}$ is monotonically increasing and converging to $L$ , we have $S_{2n%2B1} \leq L$ . Hence we have 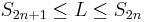$S_{2n%2B1} \leq L \leq S_{2n}$ for all n.

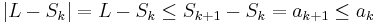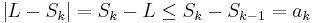Therefore if k is odd we have $|L - S_k| = L - S_k \leq S_{k%2B1} - S_k = a_{k%2B1} \leq a_k$ , and if k is even we have $|L-S_k| = S_k - L \leq S_k - S_{k-1} = a_k$ .

Literature

Knopp, Konrad, "Infinite Sequences and Series", Dover publications, Inc., New York, 1956. (§ 3.4) ISBN 0-486-60153-6

Whittaker, E. T., and Watson, G. N., A Course in Modern Analysis, fourth edition, Cambridge University Press, 1963. (§ 2.3) ISBN 0-521-58807-3

Last, Philip, "Sequences and Series", New Science, Dublin, 1979. (§ 3.4) ISBN 0-286-53154-3

References

^ Beklemishev, Dmitry V. (2005). Analytic geometry and linear algebra course (10 ed.). FIZMATLIT.

External links

Weisstein, Eric W., "Leibniz Criterion" from MathWorld.